El Hexágono y su area

En geometría, un hexágono es un polígono de seis lados y seis vértices. 

Propiedades 

Un hexágono tiene 6 lados y 9 diagonales, resultado que se puede obtener aplicando la ecuación general para determinar el número de diagonales de los polígonos, ; siendo el número de lados , tenemos:

La suma de todos los ángulos internos de cualquier hexágono es 720 grados ó 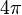 r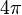adianes. 

HEXÁGONO REGULAR. 

El hexagono regular tiene las siguientes propiedades:

Ángulos internos son congruentes midiendo 120° ó 2\pi/3 rad

Cada ángulo externo del hexágono regular mide 240° ó 4\pi/3 rad.

Está íntimamente relacionado con los triángulos equiláteros:

Uniendo cada vértice con su opuesto, el hexágono regular queda dividido en seis triángulos equiláteros.

Numérense los vértices de 1 a 6 siguiendo las agujas del reloj. Uniendo los vértices impares se obtiene un triángulo equilátero; uniendo los vértices pares se obtiene otro.

Se puede teselar el plano con hexágonos sin dejar ningún hueco.

Al multiplicar la longitud l de un lado de un hexágono regular por seis (el número de lados n del polígono) obtendremos la longitud de su perímetro P.

P = n\cdot t = 6\ t

Si se conoce la longitud del apotema a del polígono, una alternativa para calcular el área es:

A = \frac{P\cdot a}{2} = \frac{6t\cdot a}{2} = 3t \cdot a

o

A = 2\sqrt{3}\cdot a^2

Si sólo conocemos el lado t podemos calcular el área con la siguiente fórmula:

A = \frac{3\sqrt{3}}{2}t^2

Construcción geométrica[editar · editar fuente]

Construcción geométrica de un hexágono regular.

Un hexágono regular puede construirse utilizando únicamente una regla y compás:

Dado un punto O cualquiera, trazar una circunferencia cuyo radio sea igual al lado del hexágono a construir;

Elegir un punto A sobre la circunferencia y trazar un diámetro que cruce O y A. Marcar el otro punto donde este diámetro interseca la circunferencia como D;

Apoyando el compás en el punto A, trazar un arco que cruce O, cortando a la circunferencia en dos puntos, marcados como B y F;

Apoyando el compás en el punto D, trazar un arco que cruce O, cortando a la circunferencia en dos puntos, marcados como C y E.  

tomado de: http://es.wikipedia.org/wiki/Hex%C3%A1gono