Nuestro proyecto consiste en las areas de regones sombreadas elaborandolo en cartulinas la explicacion del tema, en que consiste nuestro tabajo y explicando cada figura. y explicadas como se saca el area de cada figura..
la cual se demustra toda clase de figuras geometricas y su area sombreada. En la primera cartulina vamos hacer la explicacion de las areas de regiones sombreadas que consiste:
en pedasos de cartulinas dibujamos una figura la explicamos y hacemos como se saca el area sombreada de cada una.
para que a las personas se les haga mas facil aprender este mecanismo de las figuras geometricas.
miércoles, 4 de septiembre de 2013
miércoles, 28 de agosto de 2013
ÁREA DE UN TRIANGULO
Un triángulo, en geometría, es un polígono determinado por tres segmentos que se cortan dos a dos en tres puntos(que no se encuentran alineados, es decir: no lineales . Los puntos de intersección de las rectas son los vértices y los segmentos de recta determinados son los lados del triángulo. Dos lados contiguos forman uno de los ángulos interiores del triángulo.
Tres lados iguales.
Dos lados iguales.
Tres lados desiguales.
Tres ángulos agudos
Un ángulo recto
El lado mayor es la hipotenusa.
Los lados menores son los catetos.
Un ángulo obtuso.
Por lo tanto, un triángulo tiene 3 ángulos interiores, 3 ángulos exteriores, 3 lados y 3 vértices.
Si está contenido en una superficie plana se denomina triángulo, o trígono, un nombre menos común para este tipo de polígonos. Si está contenido en una superficie esférica se denomina triángulo esférico. Representado, en cartografía, sobre la superficie terrestre, se llama triángulo geodésico.
Clasificación de los triángulos
Los triángulos se pueden clasificar por la relación entre las longitudes de sus lados o por la amplitud de sus ángulos.
Por las longitudes de sus lados
Por las longitudes de sus lados, todo triángulo se clasifica:
- Como triángulo equilátero, cuando los tres lados del triángulo son del mismo tamaño (los tres ángulos internos miden 60 grados ó
- Los triángulos se pueden clasificar por la relación entre las longitudes de sus lados o por la amplitud de sus ángulos.
Por las longitudes de sus lados
Por las longitudes de sus lados, todo triángulo se clasifica:- Como triángulo equilátero, cuando los tres lados del triángulo son del mismo tamaño (los tres ángulos internos miden 60 grados ó radianes.)
- Como triángulo isósceles (del griego ἴσος "igual" y σκέλη "piernas", es decir, "con dos piernas iguales"), si tiene dos lados de la misma longitud. Los ángulos que se oponen a estos lados tienen la misma medida. (Tales de Mileto, filósofo griego, demostró que un triángulo isósceles tiene dos ángulos iguales, estableciendo así una relación entre longitudes y ángulos; a lados iguales, ángulos iguales1 ).
- Como triángulo escaleno (del griego σκαληνός "desigual"), si todos sus lados tienen longitudes diferentes (en un triángulo escaleno no hay dos ángulos que tengan la misma medida).
Equilátero Isósceles - Como triángulo equilátero, cuando los tres lados del triángulo son del mismo tamaño (los tres ángulos internos miden 60 grados ó
- Como triángulo isósceles (del griego ἴσος "igual" y σκέλη "piernas", es decir, "con dos piernas iguales"), si tiene dos lados de la misma longitud. Los ángulos que se oponen a estos lados tienen la misma medida. (Tales de Mileno, filósofo griego, demostró que un triángulo isósceles tiene dos ángulos iguales, estableciendo así una relación entre longitudes y ángulos; a lados iguales, ángulos iguales1 ).
- Como triángulo escaleno (del griego σκαληνός "desigual"), si todos sus lados tienen longitudes diferentes (en un triángulo escaleno no hay dos ángulos que tengan la misma medida).
 |  |  |
| Equilátero | Isósceles |
Los triángulos acutángulos pueden ser:
- Triángulo acutángulo isósceles: con todos los ángulos agudos, siendo dos iguales, y el otro distinto. Este triángulo es simétrico respecto de su altura.
- Triángulo acutángulo escaleno: con todos sus ángulos agudos y todos diferentes, no tiene eje de simetría.
- Triángulo acutángulo equilátero: sus tres lados y sus tres ángulos son iguales; las tres alturas son ejes de simetría (dividen al triángulo en dos triángulos iguales).
Los triángulos rectángulos pueden ser:
- Triángulo rectángulo isósceles: con un ángulo recto y dos agudos iguales (de 45° cada uno), dos lados son iguales y el otro diferente: los lados iguales son los catetos y el diferente es la hipotenusa. Es simétrico respecto a la altura de la hipotenusa, que pasa por el ángulo recto.
- Triángulo rectángulo escaleno: tiene un ángulo recto, y todos sus lados y ángulos son diferentes.
Los triángulos obtusángulos pueden ser:
- Triángulo obtusángulo isósceles: tiene un ángulo obtuso, y dos lados iguales que son los que forman el ángulo obtuso; el otro lado es mayor que éstos dos.
- Triángulo obtusángulo escaleno: tiene un ángulo obtuso y todos sus lados son diferentes.
| Triángulo | equilátero | isósceles | escaleno |
|---|---|---|---|
| acutángulo |  |  |  |
| rectángulo |  |  | |
| obtusángulo |
DEFINICIÓN DEL TRIANGULO
El triángulo es un polígono de tres lados.
El triángulo está determinado por tres segmentos de recta que se denominan lados, o por tres puntos no alineados llamadosvértices.
Triángulos según sus lados
Triángulo equilátero
Tres lados iguales.
Triángulo isósceles
Dos lados iguales.
Triángulo escaleno
Tres lados desiguales.
Triángulos según sus ángulos
Triángulo acutángulo
Tres ángulos agudos
Triángulo rectángulo
Un ángulo recto
El lado mayor es la hipotenusa.
Los lados menores son los catetos.
Triángulo obtusángulo
Un ángulo obtuso.
tomado de DITUTOR
EL CUADRADO Y SU AREA
El cuadrado es la figura geométrica formada por cuatro líneas rectas de igual longitud, denominadas lados, que forman ángulos perfectamente rectos en los puntos de unión entre ellas (esquinas a 90º).
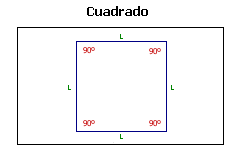
El cuadrado es una figura muy estable y de carácter permanente, asociada a conceptos como estabilidad, permanencia, honestidad, rectitud, limpieza, esmero y equilibrio.
La figura derivada del cuadrado por modificación de sus lados es el rectángulo, de propiedades análogas al cuadrado, aunque sugiere menos perfección y estabilidad.
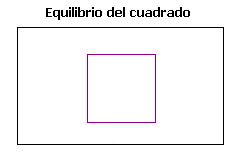
El cuadrado expresa direccionalidad horizontal y vertical, referencia primaria con respecto al equilibrio y el bienestar. Es menos sugerente y más neutro que los rectángulos, pero más sólido. Invita a mirar su centro y pasear la mirada en espiral en torno a ese punto.
El cuadrado es una figura muy estable y de carácter permanente, asociada a conceptos como estabilidad, permanencia, honestidad, rectitud, limpieza, esmero y equilibrio.
La figura derivada del cuadrado por modificación de sus lados es el rectángulo, de propiedades análogas al cuadrado, aunque sugiere menos perfección y estabilidad.
El cuadrado expresa direccionalidad horizontal y vertical, referencia primaria con respecto al equilibrio y el bienestar. Es menos sugerente y más neutro que los rectángulos, pero más sólido. Invita a mirar su centro y pasear la mirada en espiral en torno a ese punto.
Área del cuadrado
El área del cuadrado es igual a lado por lado.
Ejercicio
Calcular el área de un cuadrado de 5 cm de lado.
El Hexágono y su area
En geometría, un hexágono es un polígono de seis lados y seis vértices.
Propiedades
tomado de: http://es.wikipedia.org/wiki/Hex%C3%A1gono
Propiedades
Un hexágono tiene 6 lados y 9 diagonales, resultado que se puede obtener aplicando la ecuación general para determinar el número de diagonales de los polígonos, 
; siendo el número de lados 
, tenemos:
; siendo el número de lados , tenemos:
La suma de todos los ángulos internos de cualquier hexágono es 720 grados ó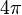 
radianes.
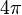radianes.
HEXÁGONO REGULAR.
El hexagono regular tiene las siguientes propiedades:
Ángulos internos son congruentes midiendo 120° ó 2\pi/3 rad
Cada ángulo externo del hexágono regular mide 240° ó 4\pi/3
rad.
Está íntimamente relacionado con los triángulos equiláteros:
Uniendo cada vértice con su opuesto, el hexágono regular
queda dividido en seis triángulos equiláteros.
Numérense los vértices de 1 a 6 siguiendo las agujas del
reloj. Uniendo los vértices impares se obtiene un triángulo equilátero; uniendo
los vértices pares se obtiene otro.
Se puede teselar el plano con hexágonos sin dejar ningún
hueco.
Al multiplicar la longitud l de un lado de un hexágono
regular por seis (el número de lados n del polígono) obtendremos la longitud de
su perímetro P.
P = n\cdot t = 6\ t
Si se conoce la longitud del apotema a del polígono, una
alternativa para calcular el área es:
A =
\frac{P\cdot a}{2} = \frac{6t\cdot a}{2} = 3t \cdot a
o
A = 2\sqrt{3}\cdot a^2
Si sólo conocemos el lado t podemos calcular el área con la
siguiente fórmula:
A = \frac{3\sqrt{3}}{2}t^2
Construcción geométrica[editar · editar fuente]
Construcción geométrica de un hexágono regular.
Un hexágono regular puede construirse utilizando únicamente
una regla y compás:
Dado un punto O cualquiera, trazar una circunferencia cuyo
radio sea igual al lado del hexágono a construir;
Elegir un punto A sobre la circunferencia y trazar un
diámetro que cruce O y A. Marcar el otro punto donde este diámetro interseca la
circunferencia como D;
Apoyando el compás en el punto A, trazar un arco que cruce
O, cortando a la circunferencia en dos puntos, marcados como B y F;
Apoyando el compás en el punto D, trazar un arco que cruce
O, cortando a la circunferencia en dos puntos, marcados como C y E.
AREA DEL ROMBO
Área del rombo
El área del rombo es igual a diagonal mayor por diagonal menor, dividido por dos.
Ejemplo
Calcular el área de un rombo cuyas diagonales miden 30 y 16 cm, y su lado mide 17 cm.
AREA DEL RECTANGULO
Área del rectángulo
El área del rectángulo es igual a base por altura.
Ejemplo
Calcular el área de un rectángulo de 10 cm de base y 6 cm de altura.
AREA DEL TRIANGULO
Área del rectángulo
El área del rectángulo es igual a base por altura.
Ejemplo
Calcular el área de un rectángulo de 10 cm de base y 6 cm de altura.
miércoles, 14 de agosto de 2013
clasificación de figuras geometrica
el circulo:En geometría euclidiana, es el lugar geométrico de los puntos del plano cuya distancia a otro punto fijo, llamado centro, es menor o igual que una cantidad constante, llamada radio. En otras palabras, es la región del plano delimitada por una circunferencia y que posee un área definida.
En castellano, la palabra círculo tiene varias acepciones, y se utiliza indistintamente círculo por circunferencia, que es la curva geométrica plana, cerrada, cuyos puntos son equivalentes del centro, y sólo posee longitud (es decir, el perímetro del círculo).Aunque ambos conceptos están relacionados, no debe confundirse la circunferencia (línea curva) con el círculo (superficie)....
ÁREA DEL CÍRCULO
El área de un circulo es igual al valor de su radio elevado al cuadrado multiplicado por Π.
|
 |
LONGITUD DE LA CIRCUNFERENCIA
La Longitud de una circunferencia es igual al valor de su diámetro multiplicado por Π.
|
L= D · Π= 2 · Π · R
|
Área del círculo
El área del círculo es igual a pi por el radio al cuadrado..
Ejemplo
La longitud de una circunferencia es 43.96 cm. ¿Cuál es el área del círculo?
tomado de DITUTOR
Suscribirse a:
Entradas (Atom)